There are no items in your cart
Add More
Add More
| Item Details | Price | ||
|---|---|---|---|
NCERT Science Notes - Class 10
Chapter 11 - Electricity
Welcome to AJs Chalo Seekhen. This webpage is dedicated to Class 10 | Science | Chapter - 11 | Electricity. In this chapter, introduces students to the fundamental concepts of electric current and circuits. It explains the relationship between voltage, current, and resistance through Ohm's Law, and dives into the intricacies of series and parallel circuits. The chapter also covers the heating effect of electric current, how electrical energy is converted into heat, and its applications. It lays the groundwork for understanding household circuits and electrical safety, making it a key chapter for grasping the basics of how electricity powers our world.
NCERT Science Notes - Class 8 Chapter 9 - Friction notes ajs, cbse notes class 10 ajslearning, cbse notes ajs, ajs notes class 10, ajslearning, ajs chalo seekhen
Questions and Answers
Problem Statement:
Q: If a current of 0.5 A flows for 10 minutes, what is the total electric charge passing through the circuit?
A: The total electric charge passing through the circuit is 300 C.
1. What makes the electric charge flow?
Questions and Answers
Q1: What is the role of potential difference in the flow of electric charges?
A1: The potential difference creates the electric pressure that causes charges to flow in a conductor, similar to how pressure differences cause water to flow in a pipe.Q2: How is electric potential difference defined?
A2: Electric potential difference (V) is defined as the work done (W) to move a unit charge (Q) from one point to another in an electric circuit.
Q3: What is the SI unit of electric potential difference and how is it defined?
A3: The SI unit of electric potential difference is the volt (V), defined as the potential difference when 1 joule of work is done to move 1 coulomb of charge.
Q4: How is a voltmeter connected to measure potential difference?
A4: A voltmeter is connected in parallel across the points between which the potential difference is to be measured.
Problem Statement:
How much work is done in moving a charge of 2 C across two points having a potential difference of 12 V?
Given:
Conclusion: The amount of work done in moving the charge of 2 C across two points with a potential difference of 12 V is 24 J.
Key Points:
Table 11.1: Symbols and Descriptions of Electrical Components
Component |
Symbol |
Description |
|---|---|---|
| Electric Cell | 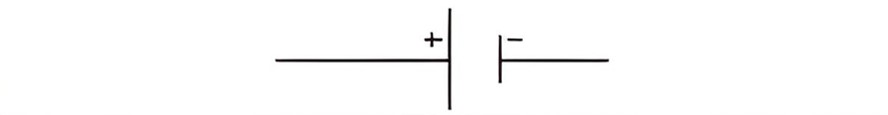 |
A single electrochemical cell that provides electrical energy. |
| Battery (or Combination of Cells) | 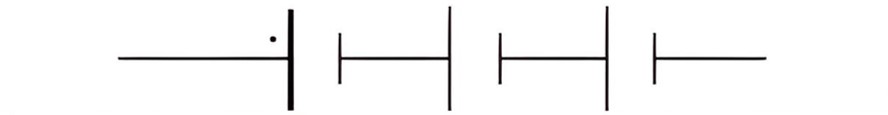 |
A combination of two or more electric cells. |
| Plug Key or Switch (Open) |  |
A device to open the circuit, preventing current flow. |
| Plug Key or Switch (Closed) |  |
A device to close the circuit, allowing current to flow. |
| Wire Joint |  |
Represents a connection between two wires. |
| Wires Crossing without Joining | 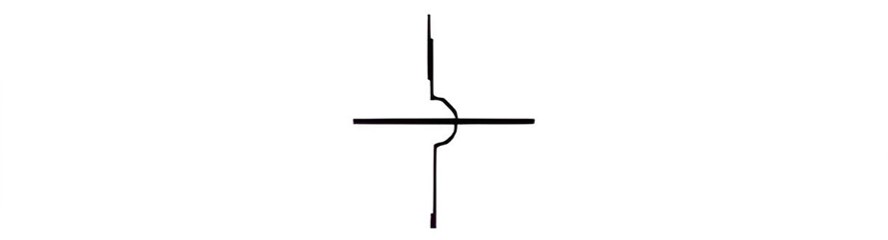 |
Indicates two wires crossing over each other without making a connection. |
| Electric Bulb | 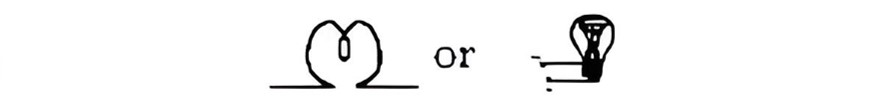 |
A device that converts electrical energy into light energy. |
| Resistor of Resistance R |  |
A component that resists the flow of electric current, measured in ohms. |
| Variable Resistance or Rheostat | 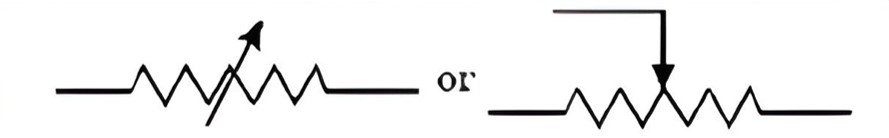 |
A resistor whose resistance can be adjusted. |
| Ammeter |  |
An instrument used to measure the current in a circuit, measured in amperes (A). |
| Voltmeter |  |
An instrument used to measure the potential difference (voltage) between two points in a circuit, measured in volts (V). |
1. Introduction to Ohm's Law:
Activity 11.1: Exploring Ohm's Law
Setup Instructions:
Conclusion
Introduction to Ohm's Law:
Ohm's Law Statement
Definition of Resistance (R)
Objective: To investigate how the current varies when different components are used in a circuit and to understand the concept of resistance in conductors.
Materials Needed
Objective: To study how resistance varies with length, cross-sectional area, and material type, and its effect on electric current.
Materials
Resistance of Conductors
Observation Summary:
Type |
Material |
Resistivity (Ω m) |
|---|---|---|
| Conductors | Silver | 1.60 × 10⁻⁸ |
| Copper | 1.62 × 10⁻⁸ | |
| Aluminium | 2.63 × 10⁻⁸ | |
| Tungsten | 5.20 × 10⁻⁸ | |
| Nickel | 6.84 × 10⁻⁸ | |
| Iron | 10.0 × 10⁻⁸ | |
| Chromium | 12.9 × 10⁻⁸ | |
| Mercury | 94.0 × 10⁻⁸ | |
| Manganese | 1.84 × 10⁻⁶ | |
| Alloys | Constantan | 49 × 10⁻⁶ |
| (Cu and Ni) | ||
| Manganin | 44 × 10⁻⁶ | |
| (Cu, Mn, Ni) | ||
| Nichrome | 100 × 10⁻⁶ | |
| (Ni, Cr, Mn, Fe) | ||
| Insulators | Glass | 10¹⁰ – 10¹⁴ |
| Hard rubber | 10¹³ – 10¹⁶ | |
| Ebonite | 10¹⁵ – 10¹⁷ | |
| Diamond | 10¹² – 10¹³ | |
| Paper (dry) | 10¹² |
Example 11.3
Problem: (a) How much current will an electric bulb draw from a 220 V source if the resistance of the bulb filament is 1200 Ω?
(b) How much current will an electric heater coil draw from a 220 V source if the resistance of the heater coil is 100 Ω?
Solution: (a)
Problem:
The potential difference between the terminals of an electric heater is 60 V when it draws a current of 4 A from the source. What current will the heater draw if the potential difference is increased to 120 V?
Solution:
Example 11.5
Problem:
Resistance of a metal wire of length 1 m is 26 Ω at 20°C. If the diameter of the wire is 0.3 mm, what will be the resistivity of the metal at that temperature? Using Table 11.2, predict the material of the wire.
Solution:
Example 11.6
Problem:
A wire of given material having length
l and area of cross-section
has a resistance of 4 Ω. What would be the resistance of another wire of the same material having length
and area of cross-section
?Solution:
Objective: To understand how potential difference distributes across resistors connected in series.
Materials Needed:
Example 11.7: Calculation with Resistors in Series
Problem:
An electric lamp with resistance
and a conductor with resistance
are connected in series to a 6 V battery (see Fig. 11.9). Calculate:
(a) The total resistance of the circuit,
(b) The current through the circuit,
(c) The potential difference across the electric lamp and conductor.
Solution:(a) Total Resistance
In a series circuit, total resistance
Rs is the sum of individual resistances:
(b) Current Through the Circuit
(c) Potential Difference Across Each Component
When resistors are connected in parallel, each resistor is connected across the same potential difference, as shown in Fig. 11.7.
Activity 11.6
Let Rp be the equivalent resistance of the parallel combination. By applying Ohm's law to the entire combination:
For each resistor:
Substituting these values into the total current equation:
Example 11.8: In the circuit diagram shown in Fig. 11.10, resistors , , and have values of 5 Ω, 10 Ω, and 30 Ω, respectively, and they are connected in parallel to a 12 V battery.
Solution:
Example 11.9
In Fig. 11.12, resistors R1=10Ω, R2=40Ω, R3=30Ω, R4=20Ω, and R5=60Ω are connected to a 12 V battery.
Solution
A battery or cell acts as a source of electrical energy, generating a potential difference that sets electrons in motion, causing current to flow through a resistor or a combination of resistors. In maintaining this current, the battery expends energy, part of which is used for useful work (e.g., rotating a fan), while the rest is often converted into heat, raising the temperature of the device.
In cases where the circuit is purely resistive (only resistors connected to a battery), the entire energy from the battery is dissipated as heat. This phenomenon is known as the heating effect of electric current and is applied in devices such as electric heaters and irons.
Derivation of Heat Produced in a Resistor
Consider a current I flowing through a resistor of resistance R, with a potential difference V across it over time t. If Q is the charge passing through the resistor, the work done to move Q through V is:
Example 11.10: An electric iron consumes power at different rates when its heating is adjusted. The power consumption is 840 W at maximum heating and 360 W at minimum heating, with a voltage supply of 220 V. We need to find the current and resistance in each case.
Solution: Using the formula for power:
Thus, the currentSolution: Heat H=100J, Resistance R=4Ω, Time t=1s, and V=?. Using the formula from Joule’s Law of Heating:
Rearrange to find I:So, the potential difference across the resistor is
.The heating effect of electric current, a phenomenon resulting from the flow of electric current through a conductor, has both undesirable and beneficial implications. While unwanted heating can alter the properties of circuit components and convert useful electrical energy into heat, it also finds numerous practical applications:
Electric power is defined as the rate at which electrical energy is consumed or dissipated in an electric circuit. It is a measure of how quickly work is done or energy is consumed in an electrical system. The power can be expressed in several forms:
Electrical Energy
Electrical energy is the product of power and time, leading to the unit of electric energy being measured in watt-hours (Wh). One watt-hour is the energy consumed when 1 watt of power is used for 1 hour. The commercial unit of electric energy is the kilowatt-hour (kWh), often referred to as a "unit."
It is a common misconception that electrons are consumed in an electric circuit. In reality, we pay for the energy supplied by electricity providers to move electrons through electrical devices like bulbs, fans, and engines. The energy we are charged for reflects the power consumed by these devices over time, not the electrons themselves.
Example 11.12 Power of an Electric Bulb
An electric bulb is connected to a 220 V generator, and the current flowing through it is 0.50 A. To find the power of the bulb, we can use the formula for electric power:
Substituting the values:Example 11.13 Cost of Operating an Electric Refrigerator
Given:
First, calculate the total energy consumed by the refrigerator over 30 days:
Now, we can find the cost to operate the refrigerator for 30 days:
NCERT Science Notes - Class 10 | Science | Chapter - 11 | Electricity
NCERT Science Notes - Class 10 | Science | Chapter - 11 | Electricity
Dedicated team provides prompt assistance and individual guidance.
Engaging visuals enhance understanding of complex concepts.
Engaging visuals enhance understanding of complex concepts.
Assess understanding and track progress through topic-specific tests



